Introduction

Below you will find the basics of the game, how my program works, and the executable and source code for a program to solve the cracker barrel peg game.

The Basics of the Game

You have an triangle made of five rows, the fifth row is made of five holes, the fourth with four, etc. for a total of fifteen holes. The game is set up with fourteen pegs, which leaves one hole empty. To start the game, you must select a peg to “jump” over an adjacent peg into an empty slot — similarly to checkers. The peg that was jumped is removed, leaving an empty hole. This process continues until you cannot make any jumps — and if you’re left with one peg, you win! If you would like to try out the game, crackerbarrel.com has a perfect java-based peg game to try out with my program.

How My Program Works

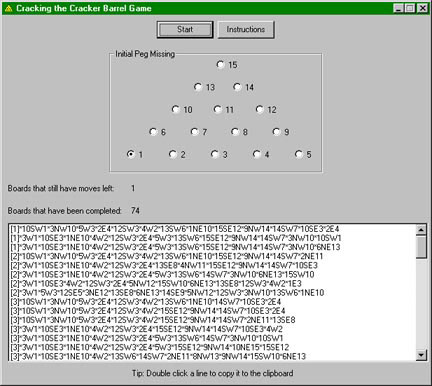
My program (screenshot below) first asks the user for the starting pin position. Whichever radio button is selected is where the first open hole is to begin the game. Once the user clicks the “Start” button, the starting board is added to an array, and the program performs the following functions:

1. Read the board that is held in the first index in the array (index 0)
2. Loop through each pin in the board and see if the pin can move
3. If the pin can move, add a new board to the array as if the pin moved to the new location
4. Continue looping through the pins until all the pins have been examined, and all the possible directions have been examined for each pin
5. If there are no possible moves for the current board, add it to the final listbox and determine the number of pins that remain
6. Remove the first index (index 0)
7. Read the new first index, check for duplicate entries in the array, continue at the top again

Each entry in the listbox begins with a number in brackets — this number is the number of remaining pins. To win the game, the items that begin with [1] are the items that have one pin remaining, and thus would win the game. After the brackets, each move is shown, separated by an asterisk. If the move is 10SW1, the pin in the 10th position (the coordinate for each pin are defined in the “initial peg missing” frame in the program) will jump southwest over the 6th position pin, and end up in the 1st position. This will remove the pin in the 6th position.

Executable and Source

• Executable (36 KB)
• Source Code (VB6, 7 KB)

Addendum

There is a known issue with the program — although it does return correct results, in some cases, the method I used to force my algorithm to become more efficient actually removes original results. In other words, there are some cases in which valid results have been removed. I would like to think that I will rewrite this program in the future, hopefully being correct, more efficient, and even possibly utilizing other forms of discovering a solution.